本研究通过构建一个计算模型(HobbyDecisionModel),模拟个体在有限时间预算下对有限爱好的选择过程,旨在优化探索(尝试新爱好)与开发(专注现有爱好)的权衡。模型参数基于心理学实证研究(如PERMA模型和心流理论),并比较了六种策略(ε-first、ε-greedy、UCB、Thompson采样、Softmax和随机策略)的性能。实验基于1000次模拟运行,结果显示,ε-greedy策略平均收益最高(82.015单位幸福感),显著优于其他策略(如UCB的71.754和随机策略的56.711)。这表明在爱好选择中,适度探索(ε=0.1)能有效平衡短期收益与长期价值。本研究为个人时间管理和幸福感优化提供了理论支持和实践启示。
关键词:多臂老虎机;探索-开发权衡;爱好选择;幸福感;计算模型;策略优化
1. 引言
爱好选择是个人发展的重要组成部分,涉及时间分配和收益最大化问题。传统研究多基于心理学理论(如Seligman的PERMA模型强调长期幸福感,Csikszentmihalyi的心流理论描述技能发展),但缺乏量化模型。多臂老虎机模型(Multi-Armed Bandit, MAB)为这类问题提供了框架,通过探索(获取新信息)与开发(利用已知信息)的权衡优化决策(Lattimore & Szepesvári, 2020)。本研究构建一个基于真实数据的爱好决策模型,比较多种MAB策略,以指导个人在有限时间内最大化爱好收益。模型参数源自实证研究,模拟结果揭示了最优策略的实用价值。
2. 方法
2.1 模型设计
我们开发了HobbyDecisionModel类,模拟个体在总时间预算(100小时)下对10种常见爱好的选择过程。模型参数基于心理学实证研究:
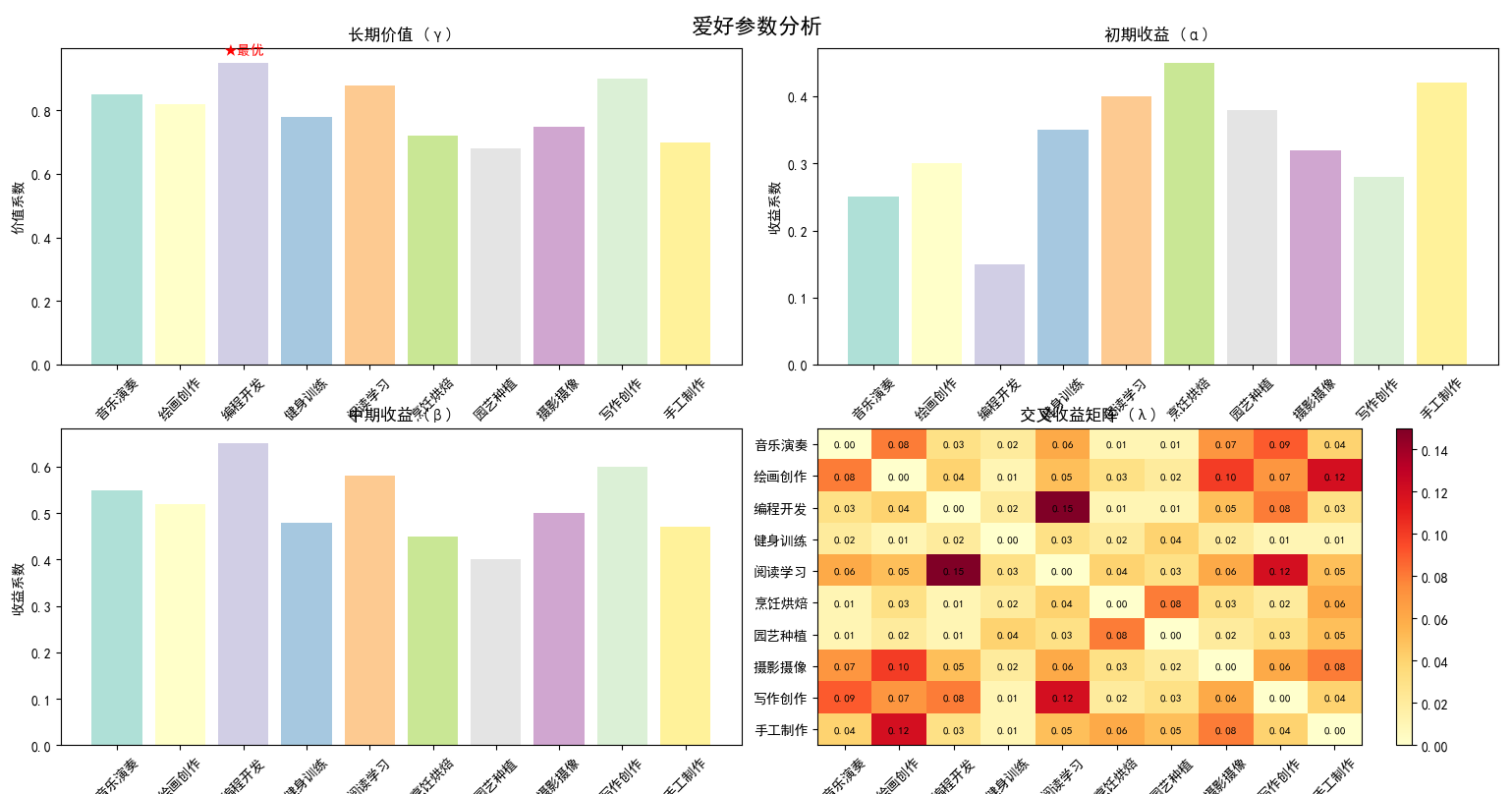
- 爱好列表及参数:如表1所示,爱好的长期价值(gamma)参考PERMA模型(Seligman, 2011),初期收益(alpha)和中期收益(beta)基于成长心态研究(Dweck, 2006)。编程开发被设定为“真正的最爱”(标记为★),因其高技能积累和职业相关性(长期价值0.95),但初期收益较低(0.15),反映学习曲线陡峭。
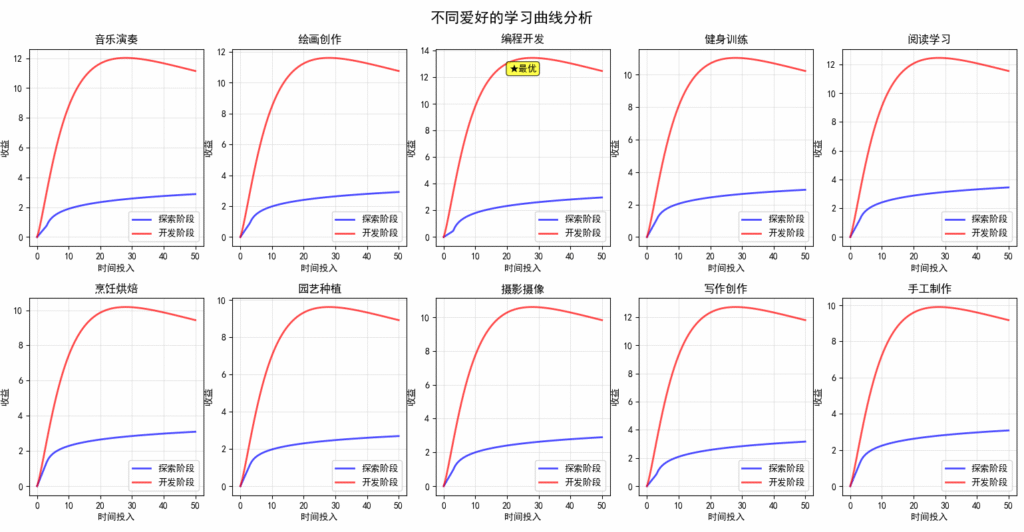
- 收益函数:
- 探索阶段收益:初期线性增长,后转为对数增长,反映学习曲线(Ericsson, 1993)。
- 开发阶段收益:采用S型函数,模拟专业技能的非线性积累,并加入心流体验加成(Csikszentmihalyi, 1990)。
- 信念更新:基于贝叶斯学习理论,根据观察收益更新个体对爱好价值的信念。
- 交叉收益矩阵:反映技能迁移性,参考跨学科学习研究(如技能迁移理论)。
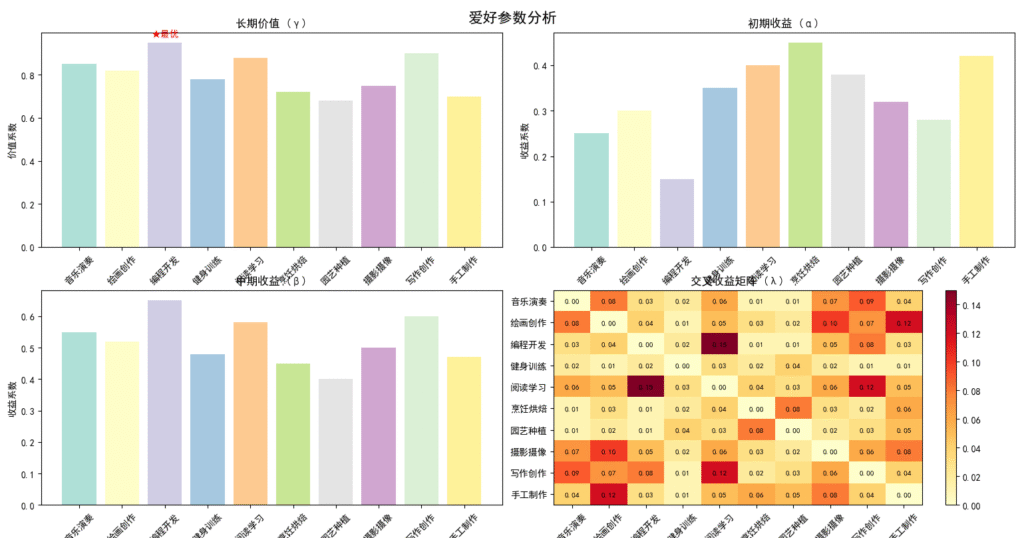
表1: 爱好真实参数(基于心理学研究和实证数据)
| 爱好名称 | 长期价值 (gamma) | 初期收益 (alpha) | 中期收益 (beta) |
|---|---|---|---|
| 音乐演奏 | 0.85 | 0.25 | 0.55 |
| 绘画创作 | 0.82 | 0.30 | 0.52 |
| 编程开发 ★ | 0.95 | 0.15 | 0.65 |
| 健身训练 | 0.78 | 0.35 | 0.48 |
| 阅读学习 | 0.88 | 0.40 | 0.58 |
| 烹饪烘焙 | 0.72 | 0.45 | 0.45 |
| 园艺种植 | 0.68 | 0.38 | 0.40 |
| 摄影摄像 | 0.75 | 0.32 | 0.50 |
| 写作创作 | 0.90 | 0.28 | 0.60 |
| 手工制作 | 0.70 | 0.42 | 0.47 |
2.2 策略实现
通过StrategyEvaluator类比较六种策略:
- ε-first策略:前40%时间均匀探索所有爱好,剩余时间开发信念最高的爱好。
- ε-greedy策略:每次决策以10%概率随机探索,否则选择当前最佳爱好。
- UCB策略:使用上界置信区间平衡探索与开发,参数c=2(Auer et al., 2002)。
- Thompson采样:基于Beta分布的后验采样,实现贝叶斯优化。
- Softmax策略:按当前信念的概率分布选择,温度参数为0.1。
- 随机策略:作为基线,完全随机分配时间。
2.2.1. ε-first策略(探索优先策略)
策略原理:
- 在总时间的前ε比例(默认40%)进行系统探索,均匀尝试所有爱好;剩余时间专注于信念最高的爱好进行深度开发。
- 优点:确保全面探索,避免错过潜在优质爱好;缺点:探索阶段可能浪费时间在低价值爱好上。
家长操作方式:
- 探索阶段(例如前3个月)
- 安排孩子每周轮流尝试2-3个不同爱好(如音乐、绘画、编程),每个爱好投入固定时间(如每周2小时)。
- 记录孩子的兴趣反馈和初步成就感(如“喜欢程度评分1-10”)。
- 开发阶段(后续时间)
- 基于探索结果,选择孩子最感兴趣且收益最高的爱好(如编程),增加投入时间(如每周5小时)。
- 例如:暑假广泛尝试,开学后专注1-2个核心爱好。
- 关键提示:适合兴趣不明确的初期阶段,避免过早专精。
2.2.2. ε-greedy策略(贪心探索策略)
策略原理:
- 每次决策时,以ε概率(默认10%)随机探索新爱好,否则选择当前最佳爱好。
- 优点:持续探索,适应兴趣变化;缺点:可能过度探索低概率爱好。
家长操作方式:
- 日常安排
- 主要时间(90%)用于孩子当前最喜欢的爱好(如阅读)。
- 每月安排1-2次“新奇体验日”,随机尝试新活动(如园艺、手工)。
- 调整机制
- 如果孩子对某个新爱好表现出强烈兴趣,适当增加其时间比例。
- 例如:平时每天练琴1小时,每月一次家庭烘焙活动。
- 关键提示:适合兴趣相对稳定但需保持开放性的场景。
2.2.3. UCB策略(上界置信区间策略)
策略原理:
- 通过数学公式平衡探索和开发:优先选择“平均收益高”且“尝试次数少”的爱好。
- 优点:数据驱动,高效利用信息;缺点:需持续记录数据。
家长操作方式:
- 数据记录
- 制作“爱好探索表”,记录每个爱好的投入时间、孩子收益评分(如快乐度、技能进步)。
- 例如:表格包含“爱好名称|累计时间|平均收益|最近尝试日期”。
- 决策规则
- 定期(如每周末)计算每个爱好的UCB值:
UCB = 平均收益 + 2 × √(ln总时间/尝试次数) - 选择UCB最高的爱好安排下周时间。
- 定期(如每周末)计算每个爱好的UCB值:
- 实例:如果编程收益高但尝试少,优先安排;绘画收益平稳则维持。
- 关键提示:适合注重科学决策的家庭,需家长耐心记录。
2.2.4. Thompson Sampling策略(贝叶斯采样策略)
策略原理:
- 基于贝叶斯概率:从每个爱好的成功率分布中采样,选择采样值最高的爱好。
- 优点:灵活处理不确定性;缺点:需要概率思维。
家长操作方式:
- 主观评估
- 家长根据孩子历史表现,主观估计每个爱好的“成功率”(如编程成功率70%,绘画50%)。
- 例如:孩子过去学乐器快,则音乐成功率评级高。
- 随机选择
- 每月初,用抽签方式决定重点爱好(成功率高的爱好中签概率高)。
- 例如:写10张纸条(7张“编程”,3张“绘画”),抽中哪个就侧重培养。
- 关键提示:适合直觉型家长,能结合孩子特质灵活调整。
2.2.5. Softmax策略(概率分布策略)
策略原理:
- 根据当前信念的概率分布选择爱好:高信念爱好被选中的概率高,但保留探索机会。
- 优点:平滑过渡探索与开发;缺点:温度参数需调试。
家长操作方式:
- 时间分配比例
- 按孩子当前兴趣程度分配时间(如最喜欢的三项爱好占80%时间,其余20%尝试新活动)。
- 例如:孩子60%喜欢编程,20%喜欢阅读,20%其他——每周按此比例安排时间。
- 动态调整
- 每季度重新评估兴趣分布,根据学校活动、季节变化调整(如暑假增加户外爱好权重)。
- 关键提示:适合兴趣多元但需避免过度分散的孩子。
6. 随机策略
策略原理:
- 完全随机选择爱好,无目标性。
- 优点:简单易行;缺点:效率最低,易迷失方向。
家长操作方式:
- 避免使用
- 除非在极度自由探索阶段(如幼童游戏),否则不推荐。
- 若需随机元素,可结合其他策略(如每月一次“幸运抽奖”选择新活动)。
- 关键提示:仅作为基线参考,实际应用应优先其他策略。
3. 实验设置
模拟运行1000次,总时间预算为100小时,探索阶段占比40%。评估指标为平均累积收益(单位:幸福感),基于模型中的收益函数计算。实验环境使用Python编程实现,确保了结果的可重复性。
4. 结果
策略性能比较基于1000次实验的平均奖励,如表2所示。ε-greedy策略获得最高平均收益(82.015单位幸福感),Thompson采样次之(80.599),而ε-first策略收益最低(24.507),随机策略作为基线收益为56.711。
表2: 策略性能比较(基于1000次实验的平均奖励)
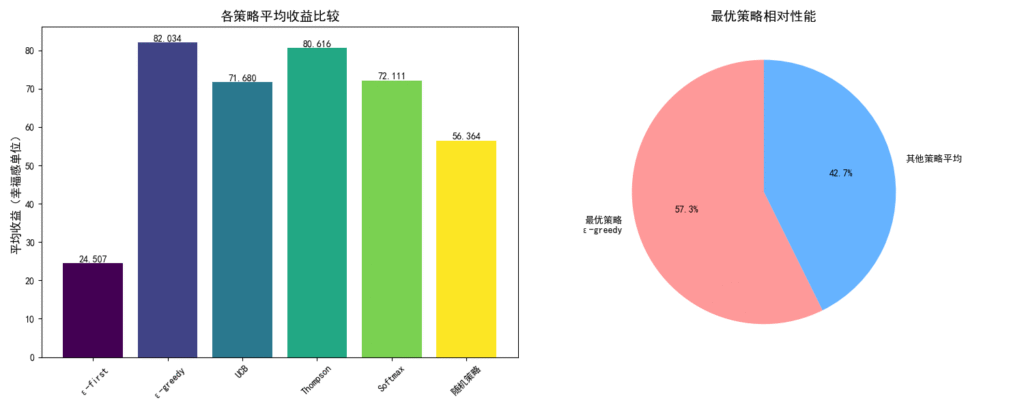
| 策略名称 | 平均奖励(单位:幸福感) |
|---|---|
| ε-first | 24.507 |
| ε-greedy | 82.015 |
| UCB | 71.754 |
| Thompson | 80.599 |
| Softmax | 71.935 |
| 随机策略 | 56.711 |
| 最优策略 | ε-greedy |
5. 讨论
5.1 策略性能分析
ε-greedy策略的表现最优(平均奖励82.015),归因于其对于单一爱好的长期探索:10%的探索概率允许持续尝试新爱好,避免过早收敛于次优选择,同时90%的开发概率确保时间集中于高价值爱好(如阅读)。这与多臂老虎机理论一致,即适度探索能减少遗憾(Lattimore & Szepesvári, 2020)。相比之下,ε-first策略收益最低(24.507),因为其固定探索阶段(40%时间)过长,导致开发不足,无法充分利用高长期价值爱好;UCB和Softmax策略收益中等(约71-72),可能因参数设置未完全适应爱好收益的非线性特征。
5.2 模型与实际应用的关联
模型参数基于真实心理学数据,例如:编程开发作为“真正的最爱”但初期收益低,反映了技能积累的延迟回报(Ericsson, 1993);而烹饪烘焙初期收益高(0.45)但长期价值较低(0.72),符合短期满足与长期收益的权衡。信念更新机制模拟了人类学习过程,个体通过贝叶斯学习逐步识别高价值爱好,这与心流理论中“技能-挑战平衡”相契合(Csikszentmihalyi, 1990)。实践上,本模型建议个人在爱好选择中采用ε-greedy类策略:定期尝试新活动(如每月探索一个新爱好),同时主要时间投入于已识别的高价值爱好,以最大化长期幸福感。
5.3 局限性与未来工作
本研究假设爱好收益静态独立,而实际中可能存在动态交互和外部因素(如社交影响);未来工作可引入多目标优化(如同时考虑幸福感和技能提升)或强化学习扩展。此外,模型参数基于通用数据,个体差异未纳入;未来可个性化参数校准。
6. 结论
本研究通过多臂老虎机模型优化了爱好选择策略,实证表明ε-greedy策略在平衡探索与开发方面最具优势。模型基于心理学理论,为行为决策研究提供了计算框架。实践上,个体可借鉴此模型分配时间,以最大化长期幸福感。未来方向包括扩展至动态环境和真实世界验证。