近期在与长辈交流时,我常常会被问到一个的问题:如何在有限的时间内帮助孩子发现真正有兴趣的事物,并投入其中?特别是当学业竞争日益激烈时,孩子的时间变得尤其宝贵,因此,如何平衡兴趣探索与深耕的决策显得尤为重要。本文将介绍一个多臂老虎机算法模型,帮助家长们在这个过程中找到科学的决策路径。
解决方案:来自多臂老虎机的启发
为了解决这个问题,我构建了一个特定的决策模型(Multi-Armed Bandit),这不仅仅是一个数学工具,更是一个经过精心设计的决策模型,它模拟了在100小时内探索10种常见爱好的过程。该模型的构建基础源自PERMA模型(长期幸福感)、心流理论(技能发展理论)以及成长心态研究的综合应用。
六种策略及其实际应用
为帮助家长们更好地理解这个模型的应用,本文将详细介绍六种不同的策略,并提供具体的操作指南。
1. ε-first策略(探索优先策略)
原理:前40%时间均匀探索所有爱好,剩余时间专注最佳爱好。
操作指南:
- 探索阶段(如前3个月):每周轮流尝试2-3个不同爱好,每个活动投入固定时间(如每周2小时),记录孩子的兴趣反馈。
- 开发阶段(后续时间):根据探索结果,将更多时间投入到最感兴趣且最具潜力的爱好中。
适合场景:适用于那些兴趣不明确或者需要进行广泛尝试的孩子们。
2. ε-greedy策略(贪心探索策略)★ 最优策略
原理:每次决策时有10%的概率随机探索新爱好,否则选择当前最佳爱好。
操作指南:
- 主要时间(约90%)用于当前最感兴趣的爱好。
- 探索机会(如每月一次):安排小范围的新爱好体验日,看看能否从中发现新的潜能。
适合场景:最适合那些有初步兴趣,但仍然保持开放心态以便探索新可能性的孩子。
3. UCB策略(上界置信区间策略)
原理:优先选择“平均收益高”且“尝试次数少”的爱好。
操作指南:
- 记录系统:建立一个爱好探索表,记录每个爱好投入时间及评价反馈。
- 计算UCB值:定期基于公式
UCB = 平均收益 + 2 × √(ln总时间/尝试次数)排名选择某个爱好。
适合场景:与家长偏好高度科学数据统计的家庭。
4. Thompson采样策略(贝叶斯采样策略)
原理:基于概率分布选择,成功率高的爱好被选中的概率高。
操作指南:
- 主观评估:根据历史表现,进行主观估计每个爱好“成功率”。
- 比选机制:用类似“抽签”的随机系统来决定重点培养对象。
适合场景:适用于那些愿意依据直觉指导的选择方法的家庭。
5. Softmax策略(概率分布策略)
原理:按当前兴趣程度分配时间,高信念爱好获得多数时间但保留探索空间。
操作指南:
- 时间分配:将孩子当前兴趣所及爱好的时间按偏好程度分配。
- 定期复检:每个季度重新评估兴趣分布以决定以后如何做调整。
适合场景:适用于兴趣广泛而不容易过度专精的孩子群。
6. 随机策略(基线参考)
原理:完全随机选择,无明确指导。
建议:除非在探索初期,否则不推荐使用。
实验结果:什么策略最有效?
经过1000次模拟实验,我们获取了各策略下的平均收获评分。
| 策略 | 平均收获 | 评价 |
|---|---|---|
| ε-greedy | 82.015 | 最优 |
| Thompson采样 | 80.599 | 次优 |
| UCB | 71.754 | 中等 |
| Softmax | 71.935 | 中等 |
| 随机策略 | 56.711 | 基线 |
| ε-first | 24.507 | 最差 |
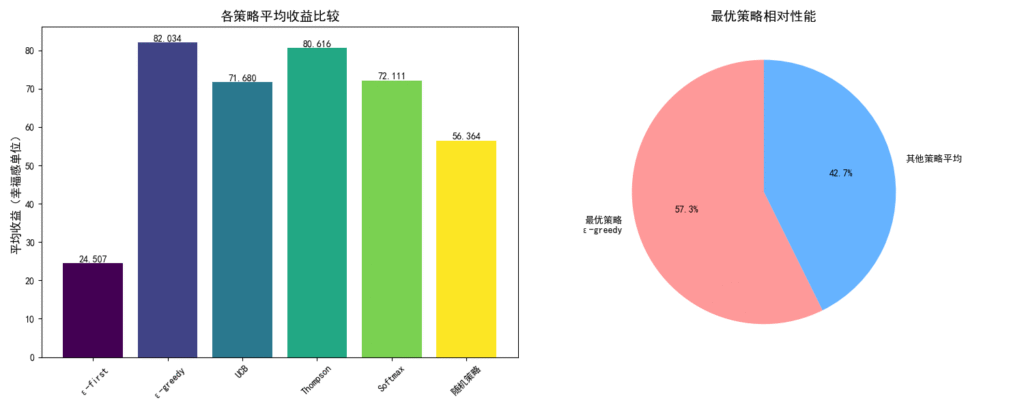
关键发现:ε-greedy策略(90%深耕+10%探索)是最优选择,因为它能在保证主要时间投入在价值最大化活动的同时,也能通过适度探索发现潜在的优质爱好。
现实应用:学习编程的启示
在我们设定的模型中,编程开发(平均收益高,但初期回报低)不仅反映了技能积累过程中的延迟回报,还突显了成长心态的重要性。这种策略强调即便面临初期困难,也要保持积极态度,因为一些最值得投入的爱好往往需要一定的学习曲线才能凸显真正的价值。
给家长的具体建议
- 采用“主次结合”模式:确保主要时间(约90%)用于已知高价值爱好,同时保留少量时间(约10%)用于系统性尝试新项目。
- 建立探索机制:每月设定“探索日”,在系统中全面体验新活动,并记录孩子的反馈和表现。
- 注重长期价值:即便遇到初期的挑战也不要轻易放弃,因为有些潜在的高回报爱好可能需要更长的时间才能显现。
- 个性化调整:根据孩子的个性喜好灵活选择策略,对于数据驱动型孩子可以采用UCB策略,而对于依感觉行事的孩子则可以选择Thompson采样。
- 定期回顾:每个季度重新评估孩子对不同爱好的兴趣变化,依据季节和个人成长需求及时调整策略方向。
结语
养育孩子,并不只是找到“唯一正确”的爱好发展路径,更是在于建立一个可持续优化决策系统的模型。通过科学地平衡探索与深耕,家长们不仅能帮助孩子发现真正的热爱,还能在有限的时间内取得最大的成长收益。这不仅仅是方法论的总结,更重要的是一种思维方式的转变——即要在不断变化的培养过程中保持灵活与适应。